David Hopwood - Cryptography - Recipient hiding

Recipient-Hiding and Related Properties for Public Key Encryption
Appendix - formal proofs

No adversary can have a greater advantage than A_opt, defined by:

A_opt.guess(r₁, ..., r_N) = 1, if r_i S₁ \ S₀ for some i 1..N
= 0, otherwise

This follows from the fact that:

when one or more of the r_i are in S₁ \ S₀, then b = 1 with probability 1.
otherwise, b has a slightly greater than 1/2 probability of being 0, but the values of the r_i give no additional information about b (so no adversary can do better than guessing b = 0 in this case).

When b = 1:

Pr[r_i 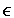S₁ \ S₀ for some i] = 1 - (|S₀| / |S₁|)^N
< 1 - (1-u)^N
< N.u (because (1-u)^N > 1 - N.u)

When b = 0:
Pr[r_i 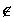S₁ \ S₀ for any i] = 1
Therefore Pr[A_opt.guess(S₀, S₁, N) = b] < (1/2.N.u) + (1/2.1)

I.e. Adv(A_opt, S₀, S₁, N) < 2.(1/2.N.u + 1/2) - 1
= N.u

So Adv(A, S₀, S₁, N) < N.u for any A, because A_opt is optimal.

Proof of Lemma 2:

Proof of security of BRH-DHAES against Chosen Plaintext Attack:

Proof of security of BRH-DHAES against Non-Adaptive Chosen Ciphertext Attack:

Proof of security of BRH-DHAES against Adaptive Chosen Ciphertext Attack:

David Hopwood
<hopwood@zetnet.co.uk>

A_opt.guess(r₁, ..., r_N)	= 1, if r_i S₁ \ S₀ for some i 1..N
	= 0, otherwise

Pr[r_i S₁ \ S₀ for some i]	= 1 - (\|S₀\| / \|S₁\|)^N
	< 1 - (1-u)^N
	< N.u (because (1-u)^N > 1 - N.u)

I.e. Adv(A_opt, S₀, S₁, N)	< 2.(1/2.N.u + 1/2) - 1
	= N.u