![[Figure showing two distributions as lines of randomly spaced dots - one of length n1, the other of length n2]](figure1.gif)
Figure 1: Distributions of RSA ciphertexts for moduli n1 and n2.
David Hopwood <hopwood@zetnet.co.uk>
Recipient-hiding is a property of public key encryption schemes that allows all information as to the public key of the recipient to be hidden from observers.
Extensions to this idea also allow public key ciphertexts to be indistinguishable from random data, or for multiple public keys to correspond to a single private key, without allowing the public keys to be linked. These properties have applications to steganography and anonymous communication. A formal security model for these properties is described, together with several schemes based on Diffie-Hellman and RSA that are provably secure in this model.
As an example of a scheme that is not recipient-hiding, consider RSA: each user Ui has a public key pki = (ni, ei) such that all the ni are distinct 1. Encrypting with pki gives ciphertexts that, for the purpose of this attack, can be treated as being uniformly distributed random integers in the range 0..ni-1.
If two public keys have moduli n1 and n2 that are not too close together, the corresponding ciphertext distributions will be distinguishable, as shown in Figure 1. If moduli are chosen at random (as they normally would be for standard RSA), then given sufficient messages encrypted to a given unknown key, and a set of keys that could have been used, an attacker can determine with high probability which key was actually used (and can rule out some of the other keys with certainty).
![[Figure showing two distributions as lines of randomly spaced dots - one of length n1, the other of length n2]](figure1.gif)
Figure 1: Distributions of RSA ciphertexts for moduli n1 and n2.
Similar attacks are possible for discrete log-based cryptosystems that use a different modulus (or more generally, a different finite group or subgroup) for each user. There seem to be two possible approaches to preventing these attacks:
In order to prove that a particular scheme is recipient-hiding, we need to have a formal model of precisely what that means. The model we will use takes into account adaptive chosen plaintext 2 and adaptive chosen ciphertext attacks. We have chosen to use DHAES ("Diffie-Hellman Authenticated Encryption Scheme") as the basis for our discrete-log-based schemes, because DHAES is efficient, flexible in terms of the group to be used, and has security proofs that can be easily adapted for our purposes.
| 1 | If different users share an RSA modulus, they can determine each
other's private keys; see Fact 1 in [RSA20]. |
| 2 | Adaptive chosen plaintext attacks do not normally need to be considered explicitly for public key algorithms, because the attacker is assumed to have access to the public key. In the case of recipient-hiding, the security property we are testing is whether an attacker can determine which public key was used, and so this key cannot be given in advance. Instead, the attacker will be given an encryption oracle. |
In the case of symmetric ciphers, the ciphertext is often assumed to "look random", and the ability to distinguish ciphertext from random (called a "distinguisher attack") is commonly taken to indicate a weakness in the cipher. For a block cipher in a standard chaining mode (e.g. CBC, CFB or OFB) or for an additive stream cipher, these are indeed valid assumptions, but more generally, the definition of a semantically secure symmetric cipher does not require that ciphertext be uniformly distributed. This also does not hold for typical public key ciphers.
The term "steganography" describes techniques that attempt to hide data by making it appear to be something else. A simple form of this would be to hide text in the low order bits of raw audio data, which would not result in any immediately obvious change to the recorded sound. (In practice, more sophisticated techniques are needed in order to prevent attacks that detect patterns in the low-order bits of real audio files, that would not be present in the steganographically modified files if these bits are simply replaced. Similar problems occur for images and other file types. Details are beyond the scope of this paper, but see [need ref].)
[[define target distribution]]
In many applications either the target distribution is uniformly random, or a uniform random distribution can be used as an intermediate step. In particular, any steganographic application that attempts to hide encrypted data will already need to be able to go from a uniform distribution to the target distribution. Without loss of generality, then, we only need to consider how to produce public key ciphertexts that are uniformly random; the problem of how to massage these into the required target distribution (if different from uniform) can be treated as a separate problem.
If Alice uses a single key pair and includes the public key in each message, then the messages can be linked; an observer is likely to infer that they were all sent by the same person [footnote: forgery doesn't matter in this case] Alice could use a separate key pair for each communication, but that would require her to maintain many different key pairs, and to try decrypting incoming messages with each of them. It would be far more convenient to be able to use a single private key, that corresponds to many unlinkable public keys. Key blinding allows exactly that.
| Scheme | Key blinding? | Steganographic? | Common parameters? | Based on |
| RH-DHAES | No | No | Yes | DHP |
| SRH-DHAES | No | Yes | Optional | DHP |
| BRH-DHAES | Yes | No | Yes | Decisional DHP |
| BSRH-DHAES | Yes | Yes | Yes | Decisional DHP |
| SRH-RSA-OAEP | No | Yes | No | RSAP |
[DHAES] explains this approach as follows:
Let S be an encryption scheme which makes use of a primitive P, and let AS be an adversary which attacks S. To show the security of S one converts AS into an adversary AP which attacks P. Ideally, AP should use the same computational resources as AS and, with this investment in resources, AP should be just as as successful in attacking P as AS was successful in attacking S. This way "practical" attacks on P imply practical attacks on S, and so the assumed absence of practical attacks on P implies the absence of practical attacks on S.As an example, consider the following definitions for a symmetric cipher:To quantify how close to this ideal we come we define the success probability of AP attacking P, we define the success probability of AS attacking S, and then we give concrete formulas to show how AP's computational resources and success probability depend on AS's computational resources and success probability. These formulas measure the demonstrated security. By giving explicit formulas we make statements which are more precise than those that are given in doing asymptotic analyses of reductions.
Let SYM = (SYM.encrypt, SYM.decrypt) be a symmetric encryption scheme with key space KEY:SYM.encrypt is a non-deterministic function, which we model by defining Coins as the set of possible random inputs. Given a non-deterministic functionSYM.encrypt : KEYand let A be an adversary.PT
Coins
CT
SYM.decrypt : KEYCT
PT
f : ...the Coins argument may be omitted to denote the distribution given by applying f. The notation "xCoins
...,
 R f(...)"
means that x is chosen at random from the distribution
{ f(..., coins) : coins
R f(...)"
means that x is chosen at random from the distribution
{ f(..., coins) : coins  R Coins }.
[Note that in all of our security definitions, random number generators will
not be modelled explicitly, and are assumed to produce output that is
indistinguishable by an adversary from a uniformly random independent
distribution. Modelling them explicitly probably wouldn't help
much: we already know that the RNG has to be secure, and it would
complicate the definitions considerably.]
R Coins }.
[Note that in all of our security definitions, random number generators will
not be modelled explicitly, and are assumed to produce output that is
indistinguishable by an adversary from a uniformly random independent
distribution. Modelling them explicitly probably wouldn't help
much: we already know that the RNG has to be secure, and it would
complicate the definitions considerably.]
The advantage of A in attacking the semantic security of SYM under adaptive chosen plaintext attack, is defined as:This definition of advantage corresponds to the following experiment:
AdvCPA(A, SYM) = 2.Pr[ K R KEY;
(P0, P1, state) := A.find(SYM.encryptK); b R {0, 1};
C R SYM.encrypt(K, Pb);
A.guess(SYM.encryptK, C, state) = b] - 1
It turns out that this "find-then-guess" definition, where the adversary chooses two plaintexts and has to determine which of them was encrypted, is equivalent to testing whether the adversary can find any information at all from the ciphertext (see [FindThenGuess]). Following [DHAES], we will also use a modified form of this type of definition for public key ciphers.
In an approach that only considered asymptotic security, we would define SYM in terms of some security parameter t, and say that SYM is secure (in this attack model) if t can be chosen to make AdvCPA(A, SYM) negligably small (say less than 2-t) for any A.
The security of SYM is defined by the functionInSecCPA(SYM, t,where the maximum is taken over all adversaries A running in time at most t, asking queries which total at most, m, m') = maxA {AdvCPA(A, SYM)}
bits, and whose outputs P0 and P1 have length at most m bits, and m' bounds the length of a SYM.encrypt-produced ciphertext whose plaintext is of length m.
| Let | PK be the set of public keys, |
| SK be the set of private keys, | |
| PT be the set of possible plaintexts, | |
| CT be the set of possible ciphertexts, | |
| Coins be the set of possible random inputs. |
A blinded-key asymmetric encryption scheme ASYM is modelled by a tuple (ASYM.encrypt, ASYM.decrypt, ASYM.keygen, ASYM.blind, ASYM.TIMES):
ASYM.encrypt : PKPT
Coins
CT
ASYM.decrypt : SKCT
PT
{INVALID}
ASYM.keygen : CoinsSK
PK
ASYM.blind : PKCoins
PK
ASYM.TIMES : a set (normally a range) of non-negative integers
Iff n is in ASYM.TIMES, then it is valid for a public key generated by ASYM.keygen to be blinded (using ASYM.blind) n times, and the resulting public key used for encryption.
[For example, if a scheme EXAMPLE allows keys to be blinded any number of times, but an initial public key generated by EXAMPLE.keygen cannot be used for encryption, then EXAMPLE.TIMES will be the set of all integers >= 1.]
{ (sk, pk0) = ASYM.keygen(coins) : coins
Coins },
n
ASYM.TIMES,
{ pki = ASYM.blind(pki-1, coins'i) : i
1..n, coins'i
Coins },
P
PT, coins''
Coins,
(ASYM.decrypt(sk, ASYM.encrypt(pkn, P, coins'')) = P)
AdvCPA(A, ASYM) = max { 2.Pr[ (sk, pk0) R ASYM.keygen;
pki R ASYM.blind(pki-1), for i
1..n;
(P0, P1, state) := A.find(pk0, ..., pkn); b R {0, 1};
C R ASYM.encrypt(pkn, Pb);
A.guess(pk0, ..., pkn, C, state) = b] - 1 : n ASYM.TIMES }
The adversary's advantage is calculated based on the following experiment:
Note that the success probability is taken over the random choices in blinding,
as well as the initial key generation and encryption. AdvCPA(A, ASYM)
is the maximum advantage of A against ASYM in an adaptive chosen
plaintext attack, over all possibilities for n (the number of blinded keys
in the chain), i.e. all values of n  ASYM.TIMES.
ASYM.TIMES.
Note that it is important for the adversary to be given the whole chain of blinded public keys, rather than just the one that is being used for encryption. As a somewhat artificial, but concrete example to motivate this, consider modifying a proven-secure blinded-key encryption scheme as follows:
 y.
y.
As in [DHAES], the security of ASYM against adaptive chosen plaintext attack is defined by the function
InSecCPA(ASYM, t, m) = maxA {AdvCPA(A, ASYM)}where the maximum is taken over all adversaries A running in time + code size at most t, and whose outputs P0 and P1 have length at most m bits.
The security of ASYM against non-adaptive chosen ciphertext attack is defined as
AdvCCA1(A, ASYM) = max { 2.Pr[ (sk, pk0) R ASYM.keygen;
pki R ASYM.blind(pki-1), for i
1..n;
(P0, P1, state) := A.find(ASYM.decryptsk, pk0, ..., pkn); b R {0, 1};
C R ASYM.encrypt(pkn, Pb);
A.guess(pk0, ..., pkn, C, state) = b] - 1 : n ASYM.TIMES }
InSecCCA1(ASYM, t, q,where the maximum is taken over all adversaries A running in time + code size at most t, making at most q queries to its decryption oracle, these queries totaling at most, m) = maxA {AdvCCA1(A, ASYM)}
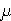 bits, and whose
outputs P0 and P1 have length at most m bits.
bits, and whose
outputs P0 and P1 have length at most m bits.
The only difference from the chosen-plaintext-only case is that the adversary is given a decryption oracle (ASYM.decryptsk) in the find stage. This is based on definition 7 from [DHAES], adapted for blinded keys.
The security of ASYM against adaptive chosen ciphertext attack is
AdvCCA2(A, ASYM) = max { 2.Pr[ (sk, pk0) R ASYM.keygen;
pki R ASYM.blind(pki-1), for i
1..n;
(P0, P1, state) := A.find(ASYM.decryptsk, pk0, ..., pkn); b R {0, 1};
C R ASYM.encrypt(pkn, Pb);
A.guess(ASYM.decryptsk, pk0, ..., pkn, C, state) = b] - 1 : n ASYM.TIMES }
InSecCCA2(ASYM, t, q,where the maximum is taken over all adversaries A running in time + code size at most t, making at most q queries to its decryption oracle, these queries totaling at most, m) = maxA {AdvCCA2(A, ASYM)}
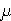 bits, and whose
outputs P0 and P1 have length at most m bits.
bits, and whose
outputs P0 and P1 have length at most m bits.
Again, this is a straightforward adaptation from definition 8 of [DHAES].
Now we define new security properties for blinded-key encryption and recipient hiding (based on the same approach to modelling security):
Note that giving the hypothetical adversary the blinded public keys directly results in a stronger security property than giving the adversary only ciphertexts, because given the public keys, the attacks can generate its own ciphertexts corresponding to arbitrary chosen plaintexts.
However, we must be careful to account for all possibilities in the relationship between the public keys involved. In the figure below, X and Y are the public keys of two newly generated key pairs, A and B are keys obtained by blinding X and Y some number of times, and Z is a blinded version of either A or B. Loosely speaking, the adversary's advantage is based on the probability of it being able to guess which key Z was blinded from.
![[Figure showing keys X, Y, A, B, Z as described above, with arrows between indicating blinding]](figure2.gif)
Figure 2: Example of relationships between blinded keys.
Only one possible case is shown in the figure; it is also possible
for Z to be one of the original keys X or Y, if keys generated by
ASYM.keygen can be used directly for encryption (i.e. when 0
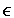 ASYM.TIMES).
In general, all valid combinations for the
number of steps between X and Z, and between Y and Z must be
considered; the overall advantage of the adversary is the maximum
advantage for any of these combinations.
ASYM.TIMES).
In general, all valid combinations for the
number of steps between X and Z, and between Y and Z must be
considered; the overall advantage of the adversary is the maximum
advantage for any of these combinations.
More precisely, for each combination, the adversary's advantage is calculated based on the following experiment:
For this security property the adversary is not given a decryption oracle (i.e. cannot perform chosen ciphertext attacks). If a decryption oracle were allowed, then it would not be possible to prove the security of public key blinding for any scheme, because that would enable asking the owner of one of the private keys whether a message can be validly decrypted - which would immediately give away whether the public key used for encryption corresponds to that private key. I.e. this type of attack must be prevented at the protocol level, rather than by the encryption scheme. This should not be too much of a problem for protocols that are specifically designed to support anonymity.
[It is still useful for chosen ciphertext attacks to be considered for message privacy, since that protects the confidentiality of messages even when the anonymity of a recipient has been broken, or the mechanism for preventing chosen ciphertext attacks at the protocol level fails (i.e. it provides defense in depth).]
The advantage of an adversary A in attacking the public key blinding of ASYM is therefore defined as
The security of ASYM for public key blinding is
AdvBlind (A, ASYM) = max { 2.Pr[ (skX, pkX0) R ASYM.keygen;
(skY, pkY0) R ASYM.keygen;
pkXi R ASYM.blind(pkXi-1), for i
1..nX;
pkYi R ASYM.blind(pkYi-1), for i
1..nY;
b R {0, 1};
pkZ = { pkXnX, if b = 0 pkYnY, if b = 1 A.guess(pkZ, (pkX0, ..., pkXnX-1), (pkY0, ..., pkXnY-1)) = b] - 1 : nX ASYM.TIMES, nY
ASYM.TIMES }
InSecBlind(ASYM, t) = maxA {AdvBlind(A, ASYM)}where the maximum is taken over all adversaries A running in time + code size at most t.
The security definition for this property has two differences from that for key blinding:
The insecurity level of ASYM for recipient hiding is
AdvHide (A, ASYM) = max { 2.Pr[ (skX, pkX0) R ASYM.keygen;
(skY, pkY0) R ASYM.keygen;
pkXi R ASYM.blind(pkXi-1), for i
1..nX;
pkYi R ASYM.blind(pkYi-1), for i
1..nY;
b R {0, 1};
(skZ, pkZ) = { (skX, pkXnX), if b = 0 (skY, pkYnY), if b = 1 A.guess(ASYM.encryptpkZ, ASYM.decryptskZ, (pkX0, ..., pkXnX), (pkY0, ..., pkYnY)) = b] - 1 : nX ASYM.TIMES, nY
ASYM.TIMES }
InSecHide(ASYM, t, q,where the maximum is taken over all adversaries A running in time + code size at most t, making at most q queries in total to its encryption and decryption oracles, these queries totaling at most) = maxA {AdvHide(A, ASYM)}
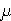 bits.
bits.
A recipient-hiding encryption scheme need not support key blinding, and the recipient hiding property can be useful on its own. Here are the corresponding definitions for an encryption scheme without key blinding, modelled as a tuple (ASYM.encrypt, ASYM.decrypt, ASYM.keygen) in the obvious way:
where the maximum is taken over all adversaries A running in time + code size at most t, making at most q queries in total to its encryption and decryption oracles, these queries totaling at most
AdvHide' (A, ASYM) = 2.Pr [ (skX, pkX) R ASYM.keygen;
(skY, pkY) R ASYM.keygen;
b R {0, 1};
(skZ, pkZ) = { (skX, pkX), if b = 0 (skY, pkY), if b = 1 A.guess(ASYM.encryptpkZ, ASYM.decryptskZ, pkX, pkY) = b] - 1
InSecHide'(ASYM, t, q,) = maxA {AdvHide'(A, ASYM)}
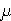 bits.
bits.
[[need explanation of relationship between blinded keys]]
![[Figure showing keys A, B, X, Y as described above, with arrows between indicating blinding]](figure3.gif)
Figure 3: Example of relationships between blinded keys.
The advantage of an adversary A in attacking the blinded-key indistinguishability of ASYM, under adaptive chosen plaintext attack is
The insecurity level of ASYM for blinded-key indistinguishability under adaptive chosen plaintext attack is
AdvIndist (A, ASYM) = max { 2.Pr[ (skZ, pkX0) R ASYM.keygen;
pkXi R ASYM.blind(pkXi-1), for i
1..nX;
pkYi = pkXi, for i 0..n;
pkYi R ASYM.blind(pkYi-1), for i
n+1..nY;
b R {0, 1};
pkZ = { pkXnX, if b = 0 pkYnY, if b = 1 A.guess(ASYM.encryptpkZ, skZ, (pkX0, ..., pkXnX-1), (pkY0, ..., pkXnY-1) = b] - 1 : nX ASYM.TIMES, nY
ASYM.TIMES, n
0..min(nX, nY-1) }
InSecIndist(ASYM, t, q,where the maximum is taken over all adversaries A running in time + code size at most t, making at most q queries to its encryption oracle, these queries totaling at most) = maxA {AdvIndist(A, ASYM)}
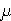 bits.
bits.
...
Recipient-hiding can be proven as follows: the form of a ciphertext is
(g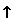 k, tag, ct) where k is chosen at random
from [1, |G|]. When common group and g parameters are used,
g
k, tag, ct) where k is chosen at random
from [1, |G|]. When common group and g parameters are used,
g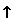 k therefore has the same distribution for
all public keys. [[unfinished]]
k therefore has the same distribution for
all public keys. [[unfinished]]
A complete description of RH-DHAES and formal security proofs are given here.
Let uProof: here(0, 1) be a security parameter.
Let R0 and R1 be uniform independent random variables over finite sets S0 and S1 respectively, where S0S1 and |S0| > (1 - u) |S1|.
The advantage of a computationally unbounded adversary A in distinguishing R0 from R1 given N > 0 samples is defined as follows:
(A may depend on S0 and S1).
Adv(A, S0, S1, N) = 2.Pr[ b R {0, 1};
r1, ..., rN R Rb;
A.guess(r1, ..., rN) = b] - 1 Then Adv(A, S0, S1, N) < N.u for any A.
It is more difficult to find an efficient steganographic encoding of some groups than others. For example, it seems to be difficult to find an encoding of elliptic curve points that cannot be distinguished from random (the point compression technique described in [HPCompression] comes close, but still retains approximately one bit of redundancy, because only points from a prime-order subgroup can be encoded).
Define a P-compact encoding as an encoding of group elements into t bits, such that P = |G| / 2t is the probability that a random t-bit string will correspond to an element of G. Also suppose that a probability u is considered negligable. Then one possibility for a steganographic encoding of a group element y is given by the following algorithm:
i := 0;
while (i < log(u) / log(P)) {
with probability P, break;
output t bits chosen uniformly at random from the set of t-bit strings that are not encodings of group elements;
i := i + 1;
}
output encoding of y;
output t.(log(u)/log(P) - i) random bits;
The probability of getting to iteration i < log(u)/log(P) without exiting the loop, is P i, therefore when i = log(u) / log(P), this probability is P log(u) / log(P) = u. It is safe to exit the loop unconditionally at that point (i.e. to put a definite limit on the maximum length of the encoding), because u is a negligable probability.
Unfortunately, although this encoding can be proven to be indistinguishable from random, it is rather inefficient unless P is close to 1. For the case of points on an elliptic curve, using the P-compact encoding described earlier with P = 1/2, the encoded length must be expanded by about 40 times to achieve a reasonable level of security.
In some cases it may be possible to omit the final padding of t.(log(u)/log(P) - i) random bits, and rely on the fact that the following parts of the ciphertext (i.e. the MAC result and symmetric cipher output) are also indistinguishable from random. Note that the expected length of the encoded group element excluding this final padding is only t / P bits (e.g. 2t bits for elliptic curves). This approach should only be used when the full ciphertext visible to an attacker is padded to a fixed total length (as is commonly done in mix-net protocols, for example), or it is embedded into another file type in such a way that the length of the full ciphertext cannot be determined. Some care is needed to ensure that bias is not introduced by a user's response to cases where the plaintext message is too long to fit in the available number of bits. For example, if a message is close enough to the length limit that whether it "fits" within this limit depends on the random choices made in the encoding process, and as a result the user repeats the process until the message fits, a bias will be introduced (the number of t-bit blocks before the first block that encodes a valid group element will be less than expected for random data).
[[unfinished]]
Consider a protocol that has two types of messages,
one public key encrypted using RH-DHAES over an elliptic curve, and another
symmetrically encrypted, where it is essential that an attacker not be able
to distinguish the two types. This can be achieved by adding a dummy header
to the symmetrically encrypted messages, which follows the same distribution
as the elliptic curve point g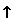 k in RH-DHAES.
A practical disadvantage of this approach is that if the protocol ever needs
to be changed not to use elliptic curves, or to use different curve parameters,
then new messages will be distinguishable from old ones.
k in RH-DHAES.
A practical disadvantage of this approach is that if the protocol ever needs
to be changed not to use elliptic curves, or to use different curve parameters,
then new messages will be distinguishable from old ones.
|
David Hopwood <hopwood@zetnet.co.uk> |